Shear variable decomposition

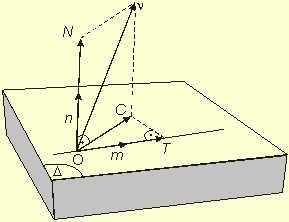
Once the cycles are separated with some method for a load history decomposition, another problem emerges, if a description of load variables on any plane is looked for as it is by multiaxial methods of fatigue life computation. The direction of normal stress/strain remains the same, but if the loading is a non-proportional one, the direction of shear stress/strain vector C can change. The shear stress changes both in magnitude and direction. The local load history on a plane can be prepared for a given node, element or isolated point via the sequence of commands Tools->Loads->Local Loads.

The resulting curve, which joins the end-points of this vector contains two necessary variables – mean shear stress and shear stress amplitude. The most of the ways of their derivations are described by Papadopoulos [Pap98]:

* Longest projection method (LPM)

* Longest chord method (LCM)

* Minimum circumscribed circle method (MCCM)

* Minimum circumscribed ellipse method (MCEM) – this solution is not described by Papadopoulos, but is preferred e.g. in [RLF04].

PragTic has a tool, where the differences of MCCM and MCEM methods can be tested. This can be run from the main menu by a sequence of commands Tools->Loads->Decompose.

This help file has been generated by the freeware version of HelpNDoc